Transcription de la BD

Panel 1
EPO: Maintenant que notre nouvelle résidence est connue, allons-y!
Capitaine: Mais à la différence de nos ancètres nous ne sommes pas experts en navigation, nous avons besoin d’aide pour y aller.

Panel 2
Alkina: Nous devons les voir en sécurité Epo.
EPO: Très bien. Balayage… Je peux guider leur vaisseau jusqu’à destination

Panel 3
Narratore: Pendant ce temps là Alkina fait connaissance avec les occupants du vaisseau…

Panel 4
Narratore: …alors qu’Epo tente d’utiliser les bases de données du vaisseau pour réparer les siennes.
Alkina: Ma tarte favorite, voulez-vous gouter?

Panel 5
Narratore: Comme leur voyage touche à sa fin…
Alkina: Nous entrons dans le système de l’étoile.

Panel 6
Alkina: Hé, pourquoi on s’arrète?

He, où est ma science?

Epo et Alkina parcourent de grandes distances au cours de leurs aventures. Naturellement, Epo possède des technologies de pointe qui lui permet de faire des voyages interstellaires rapidement. Essayons de calculer combien de temps cela prendrait pour parcourir une distance donnée à une vitesse définie. Après cela vous aurez l’opportunité d’effectuer un calcul vous même.

Pendant les années ’60 et ’70, les astronautes du programme spatial d’Apollo ont voyagé de la terre à la lune. Afin d’échapper à la pesanteur de la terre, les fusées ont été conçues pour voyager à environ 11 km/sec, ce qui est plus de 39600 kilomètres par heure! Imaginons que nous voulons faire un voyage en vaisseau rapide vers le soleil, qui est a environ 150 millions de kilomètres de la Terre. Combien de temps nous faudrait-il pour y arriver? Pour calculer le temps de voyage, nous devons diviser la distance parcourue par la vitesse à laquelle nous voyageons:

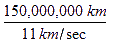= 13,636,363 secondes, soit 158 jours.

Pouvez-vous employer cette même méthode pour déterminer combien de temps Epo et Alkina mettraient pour atteindre leur destination à une distance de 3.25 années-lumière s’ils voyageaient à la vitesse des astronautes d’Apollo? Vous pouvez utiliser la calculatrice ci-dessous pour convertir les années lumières en kilomètres. (Notez: 4.12e+5 = 412.000. De plus, il y a 86.400 secondes en un jour.)

Si vous pensez que vous avez la réponse, envoyer un mel à Epo et Alkina à edeon@sonoma.edu avec votre réponse et nous vous dirons si votre réponse est correcte!