Tanscripción de Comic

Pánel 1
Alkina: Entonces, ¿dices qué estamos en la Vía Láctea al igual que la Tierra?

Pánel 2
EPO: Afirmativo
Alkina: Eso significa que la Tierra será fácil de encontrar, ¿cierto?
EPO: Negativo. La corrupción de las bases de datos borró la posición del planeta Tierra dentro de la Vía Láctea.

Pánel 3
Alkina: Dijiste que la Tierra tenía habitantes que “navegaban los océanos”, así que quizá debamos buscar planetas con océanos.
EPO: Buscaré primero entre todos los objetos a 10 pársec a la redonda.

Pánel 4
Alkina: Me pregunto cuánto tiempo hemos estado fuera.
EPO: Puede que no sea nuestro hogar. Puede que sea dónde…

Pánel 5
Alkina: ¿Qué es eso?
EPO: Escaneando. Es más pequeño que un planeta. Es una construcción artificial.

Pánel 6
Alkina: ¿Una construcción artificial? ¿Es algo hecho por gente?
EPO: Sí. Es una nave, y está acercándose.
Alkina: ¿Una nave cómo la nuestra?
EPO: Negativo.

Pánel 7
Alkina: ¡Tienes razón! ¡Es enorme! ¡¿Quién necesitaría una nave tan grande?!
EPO: Escaneando…

¿Qué significa eso?

Pársec – Es una regla de medir utilizada por astrónomos. Un pársec es igual a aproximadamente 3.3 años luz.

¡En nuestra lengua por favor!

Pársec viene de la contracción de paralaje de un segundo de arco* en inglés, parallax of one arcsecond, que describe la distancia a la cual la paralaje de un objeto es igual a un segundo de arco. Está basado en la paralaje de una estrella, por ejemplo: qué tanto parece ésta cambiar de posición en el cielo conforme la Tierra orbita alrededor del Sol. Para entender el concepto básico, coloca tu brazo estirado directo frente a ti con tu dedo pulgar apuntando hacia arriba. Viendo tu dedo pulgar, primero cierra un ojo y luego el otro, alternando entre uno y el otro. Verás cómo tu pulgar se mueve con respecto al fondo conforme cambias de un ojo al otro. Ahora mueve tu pulgar a media distancia hacia tu nariz, y realiza el mismo ejercicio. Verás que tu pulgar parece trasladarse a través de un ángulo más grande con respecto al fondo. Así es cómo funciona la paralaje. Para medir la distancia a una estrella usando la paralaje, imagina que uno de tus ojos es la posición de la Tierra en un punto en su órbita. Y el otro ojo entonces representaría la posición de la Tierra seis meses después, cuando está en el extremo opuesto de la órbita.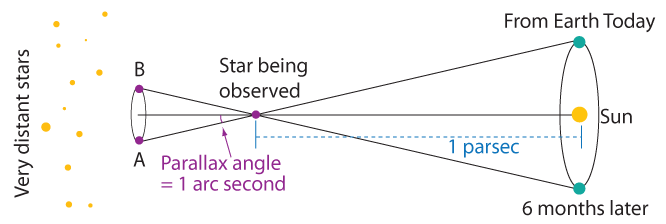

Esta imagen muestra la paralaje de una estrella cercana. Si la estrella se observa hoy en día, parecerá estar en la posición A en comparación con las estrellas lejanas que no tienen paralaje. Al cabo de seis meses, si se observa la misma estrella parecerá estar en la posición B en comparación con las estrellas distantes. Nota – Esta imagen no está a escala.

En lugar de mirar tu pulgar, imagina que eres un astrónomo midiendo cuidadosamente la posición de una estrella cuando la Tierra está en un lado del Sol y de nuevo seis meses después cuando la Tierra está del otro lado del Sol. Si la estrella está lo suficientemente cerca, verás cómo se mueve un poco de un lado al otro con respecto a las estrellas más lejanas, al igual que tu pulgar se movía con respecto al fondo. Entre más alejada esté una estrella del Sol más pequeño será el ángulo de paralaje; hay una fórmula matemática muy simple entre el ángulo de paralaje, el tamaño de la órbita de la Tierra y la distancia a la estrella. Desafortunadamente incluso para las estrellas más cercanas, el ángulo es muy pequeño. Para estrellas lejanas es tan pequeño que no puede ser medido desde la tierra; de forma que la mayoría de las estrellas no presentan un cambio debido a la paralaje. Piensa en ver el cambio de posición de tu pulgar si tu brazo fuera tan largo como un campo de fútbol.

*Si tuvieras un círculo y lo partes en 360 partes iguales cómo un pastel, cada pedazo tendría un ángulo de un grado. Si tomaras una de las 360 partes y la divides en 60 partes iguales, cada una de éstas tendría un ángulo de un minuto de arco. Al dividir estas pequeñas partes en otros 60 pedazos iguales tendríamos rebanadas de pastel con un ángulo de un segundo de arco. Ahora habrías convertido la rebanada original de pastel de un ángulo de un grado en 3600 pedazos, cada uno con un ángulo de un segundo de arco. ¡Sería una diminuta rebanada de pastel!