
Comic Transcript
Panel 1
ALKINA: Speaking of escaping the pull of gravity…what is the escape velocity of the planet?
G’SWIGT: Well, the surface gravity is 15.15 meters per second per second. Which means the escape velocity is 16.45 kilometers per second.
Panel 2
ALKINA: I thought things felt heavy here. My ship is calibrated to simulate 9.8 meters per second per second surface gravity.
G’SWIGT: Ah, then on your lost and mysterious Earth, the escape velocity is less than ours.
Panel 3
ALKINA: Yes, on Earth one needs a velocity of about 11.2 kilometers per second to escape the gravity.
Panel 4
G’SWIGT: How I would love to only have to reach 11.2 kps! That would make things so much easier for me than 16.45!
Panel 5 & 6
[Epo dodging and weaving through debris of stuff in the final two panels]
ALKINA-NARATION: That’s what rocket scientists used to say, wishing they could use Earth’s Moon as their launching point instead of Earth.
What does it mean?
escape velocity – the velocity an object must attain in order to break the gravitational bond of another object, for example, a planet.
surface gravity – the amount of gravitational acceleration an object is subjected to at the surface of a planet.
In human speak please!
A planet’s surface gravity sets the escape velocity needed to break away from the planet’s gravitational field when traveling from the planet’s surface. For any given planet, the surface gravity, g, will be equal to the gravitational constant, G, times the mass of the planet, M, divided by the radius of the planet squared.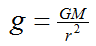
Escape velocity is equal to the square root of the quantity of two times the surface gravity, g, times the radius of the planet, r. So,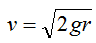
Given these two equations, can you find the radius and mass of G’swigt’s planet (answers next week)?
