Trascrizione del fumetto

Quadro 1
Alkina: Così tu dici che noi siamo nella Via Lattea, e così anche anche la Terra?

Quadro 2
EPO: Affermativo.
Alkina: Allora la Terra dovrebbe essere facile da trovare, vero?
EPO: Negativo. Un errore nel database ha cancellato la posizione della Terra nella Via Lattea.

Quadro 3
Alkina: Hai detto che la Terra ha abitanti che navigano gli oceani, quindi forse dobbiamo cercare i pianeti che posseggono oceani.
EPO: Ispezionerò per prima cosa tutti gli oggetti entro 10 parsec.

Quadro 4
Alkina: Mi domando da quanto tempo siamo via?
EPO: Potrebbe non essere casa nostra. Potrebbe essere dove noi…

Quadro 5
Alkina: Cos’e’ quello?
EPO: Ispezione. E’ più piccolo di un pianeta. E’ una costruzione artificiale.

Quadro 6
Alkina: Una costruzione artificiale? Come qualcosa fatto dagli uomini?
EPO: Si. E’ una astronave e si sta avvicinando a noi.
Alkina: Una nave come la nostra?
EPO: Negativo.

Quadro 7
Alkina: Hai ragione, è enorme! Chi avrebbe bisogno di una nave così grande?
EPO: Ispezione…

Cosa significa?

Parsec – è una unità di lunghezza usata dagli astronomi. Un parsec equivale a circa 3.3 anni luce.

Nella nostra lingua per favore!

Parsec è l’abbreviazione di parallasse di un arcosecondo*, la distanza alla quale la parallasse di un oggetto è un arcosecondo. Si basa sulla parallasse di una data stella, cioè di quanto sembra che cambi la posizione della stella nel cielo mentre la Terra orbita attorno al Sole. Per capirne l’idea base, tieni il braccio dritto di fronte a te con il pollice alzato. Guarda il tuo dito, prima chiudendo un occhio, e poi l’altro, passando alternativamente da l’uno all’altro. Così facendo vedrai il tuo dito muoversi di quà e di là rispetto allo sfondo. Adesso muovi il tuo dito indietro a metà distanza rispetto al tuo naso e ripeti l’esercizio. Vedrai che il tuo dito sembrerà muoversi di un angolo maggiore rispetto al precedente. Così lavora la parallasse. Per misurare la distanza di una stella usando la parallasse immagina che uno dei tuoi occhi sia la posizione della Terra in un punto della sua orbita. L’altro occhio sia allora la posizione della terra sei mesi dopo, quando è nel punto opposto dell’orbita.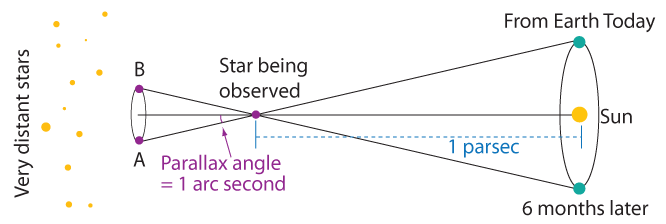

Questa immagine illustra la parallasse di una stella vicina. Se la stella è osservata oggi, apparirà nella posizione A rispetto alle stelle distanti che non hanno parallasse. Osservata sei mesi più tardi la stella apparirà nella posizione B rispetto alle stelle lontane. (Nota: l’immagine non è in scala.)

Invece di guardare il tuo dito, immagina di essere un astronomo che sta misurando accuratamente la posizione di una stella, quando la terra è su un lato del sole e nuovamente sei mesi più tardi quando la terra è sull’altro lato del sole. Se la stella è abbastanza vicina, la vedrai spostarsi lentamente rispetto alle stelle nello sfondo, proprio come si muoveva il tuo dito nell’esperimento precedente. Più lontana dal Sole è la stella, più piccolo è l’angolo di parallasse; c’è una relazione matematica molto semplice tra l’angolo di parallasse, la dimensione dell’orbita della Terra e la distanza della stella. Questa relazione permette agli astronomi di dedurre la distanza di ciascuna stella che mostra una parallasse. Sfortunatamente, anche per le stelle abbastanza vicine l’angolo è molto piccolo. Per le stelle distanti è così piccolo che non può essere misurato da terra, così la maggior parte delle stelle non mostra nessun spostamento di parallasse: Pensa a come vedresti muovere il tuo dito se il tuo braccio fosse lungo come un campo di calcio.

*Se prendi un cerchio e lo suddividi come una torta in 360 parti uguali, ciascuna parte avrà un angolo di un grado. Se prendi una di queste 360 parti e la dividi in ulteriori 60 parti, ciascuna di queste parti avrà un angolo di un arcominuto. Dividendo ciascuna di queste parti nuovamente in 60 parti avrai una fetta di torta che ha un angolo di un arcosecondo. Così facendo hai trasformato il pezzo di torta originale (con un angolo di un grado) in 3600 pezzi (ciascun pezzo con un angolo di un arcosecondo). Una fetta di torta veramente sottile!