Transcription de la BD

Panel 1
Alkina: Donc tu dis que nous sommes dans la Voie Lactée, et que la Terre aussi?

Panel 2
EPO: Affirmatif.
Alkina: Alors la Terre devrait être facile á trouver?
EPO: Négatif. La corruption des bases de données a effacé la position de la Terre dans la Voie Lactée.

Panel 3
Alkina: Tu disais qu’il y avait des “marins” sur la Terre. Tu devrais scanner pour trouver quelles planètes ont des océans.
EPO: Je vais d’abord scanner tout objet á moins de 10 parsecs.

Panel 4
Alkina: Je m’demande depuis combien d’temps on est parti?
EPO: Nous venons peut-être pas de là. C’est peut-être lá où…

Panel 5
Alkina: C’est quoi ça?
EPO: Scanne. C’est plus petit qu’une planète. C’est une construction artificielle.

Panel 6
Alkina: Construction artificielle? Fabriqué par des gens?
EPO: Oui. C’est un vaisseau, et il s’approche.
Alkina: Un vaisseau comme le notre?
EPO: Négatif.

Panel 7
Alkina: En effet, mais qui a besoin d’un vaisseau, si gigantesque!?
EPO: Scanne…

Qu’est ce que cela signifie?

Le Parsec – est une unité de longueur utilisée en astronomie. Un parsec est ègal à environ 3,3 années lumières.

En langage courant!

Le parsec est l’abréviation de parallaxe de une seconde , c’est la distance à laquelle est la parallaxe d’un objet est de une seconde d’arc. Il est basé sur la parallaxe d’une étoile donnée, c.-à-d., son mouvement angulaire apparent dans le ciel lorsque la Terre fait une-demie orbite autour du Soleil. Pour comprendre l’idée fondamentale, tendez votre bras droit devant votre visage avec votre pouce pointé vers le haut. Tout en regardant votre pouce, fermez d’abord un oeil, puis l’autre, alternant d’un oeil à l’autre. Vous verrez votre pouce se déplacer de droite à gauche par rapport aux objets qu’il y a derrière. Maintenant réduisez la distance de votre pouce à votre visage d’environ la moitié en pliant votre bras et faites le même exercice. Vous verrez que votre pouce semble se déplacer d’un angle beaucoup plus grand par rapport à ce qu’il y a derrière. C’est comment ça que fonctionne la parallaxe. Pour mesurer la distance d’une étoile utilisant la parallaxe, imaginez qu’un de vos yeux représente la position de la Terre à un certain point dans son orbite. Votre autre oeil représente alors la position de la Terre six mois plus tard à l’ opposé de son orbite.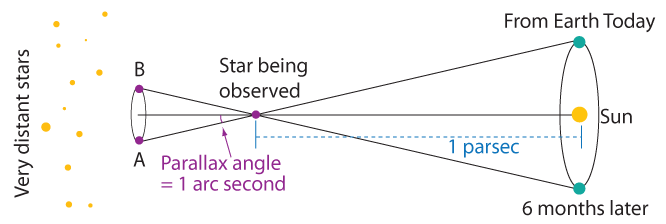

Cette image illustre la parallaxe d’une étoile voisine. Si on observe aujourd’hui l’étoile, elle semble être en position A par rapport aux étoiles éloignées qui n’ont aucun parallaxe. Quand on observe l’étoile six mois plus tard, elle paraît être en position B par rapport aux étoiles éloignées. (Note: cette image n’est pas à l’échelle réelle.)

Au lieu d’observer votre pouce, imaginez que vous êtes un astronome mesurant attentivement la position d’une étoile de la Terre quand elle est d’un côté du soleil et six mois plus tard quand la Terre est de l’autre côté du soleil. Si l’étoile est assez près, vous la verrez se déplacer dans les deux sens légèrement par rapport aux étoiles de fond, tout comme votre pouce se déplaçait par rapport à ce qu’il y avait derrière. Plus l’étoile est loin du Soleil, plus son angle de parallaxe est petit; il y a une relation mathématique très simple entre l’angle de parallaxe, la taille de l’orbite terrestre, et la distance d’une étoile. Ce rapport permet aux astronomes de déduire la distance de toutes les étoiles qui ont une parallaxe. Malheureusement, même pour les étoiles tout à fait voisines l’angle est très petit. Pour des étoiles très éloignées, l’angle est si petit qu’il ne peut pas être mesuré de la Terre. Ainsi la plupart des étoiles ne montrent aucun décalage et n’ont pas de parallaxe visible: Pensez à l’exercice d’observation avec votre pouce, si votre bras était aussi long qu’un terrain de foot, vous ne verriez aucun décalage.

* Prenez un cercle et découpez le comme un gâteau en 360 morceaux égaux, chaque morceau aurait un angle de un degré. Prenez un de ces 360 morceaux et divisez le en 60 morceaux, chacun de ces morceaux aura un angle d’une minute d’arc. Si on divise a nouveau chacun de ces morceaux en 60 morceaux, cela donnerait une part de gâteau d’un angle d’une seconde d’arc. Avec tout cela, vous avez transformé le premier morceau (avec angle d’un degré) en 3600 morceaux (chaque morceau avec un angle d’une seconde d’arc). C’est une part minuscule de gâteau!